
数列题是GRE数学中令很多考生头痛的一类题目,两项关系疯狂组合变换才能够造出一个等差数列或者等比数列。高中留下的阴影使得同学们在考试过程中一看到数列题,内心就咯噔一下,暗暗想着“完了,今天也是没有考到Q170的我。”
如果你也有同样的烦恼,不妨将这篇文章看下去。
在我们高中的学习中,数列题往往是以简答题形式出现的,需要给出完整的演算步骤。而GRE数学就不一样了,我们要的只是最后的一个结果,所以代入算数也好,猜测也罢,只要能选出正确的答案来任务就算完成了。今天小姜老师就要教给大家在考试过程中如何对数列题进行“有理有据”的猜测。
在猜答案之前,我们得知道数列题的分类,因为每一类题目都有一种解题思路。
数列题主要分为三类:
基本等差等比数列题
两项关系题(小项题)
第100项题/前100项和(大项题)
基本等差等比数列题
首先第一类,基本等差等比数列题,这种题没什么好说的,公式背下来整就完事儿了,但是需要注意等差等比数列分别有两个特殊性质,这两个特殊性质熟悉的情况下可以直接使用
等差数列中有
am+an=2a(m+n)/2
例:a1+a9=2a5
a4+a12=2a8
看题目:

如果不知道这一性质,我们可能需要将等差数列的通项公式列出并进行相应推倒,但是知道这个性质之后我们可以快速求出a2+a4=2a3, 且我们知道a1+a3+a5=2a3+a3=3a3=27, 因此a3=9,2a3=18。解题速度会相应变快很多。
两项关系题(小项题)
等比数列中的特殊性质则是
am*an=[a(m+n)/2]^2
例:a1*a9=(a5)^2
a4*a12=(a8)^2
第二类就是我们所说的两项关系,这类题型通常是下面例举的例题形式的。

这类题目在我们高中过程中解题方法就是经过形式的变换构造等差或者等比数列。构造数列这个能力对于数学基础比较好的同学相对容易,但对于很久没有做过相似题目的同学就比较困难了(这道题我们可以在等式两边同减1,构造成一个首项为2,公比为2的等比数列,因为考试时候用这种办法比较费时,在这里不展开讨论,感兴趣的同学可以尝试解答)。
对于这种两项关系图,我们要做的事就是根据题目中两项关系,直接将前5项计算出来,并根据问法写出数字,直接找数字规律,一般这些数字的规律都比较明显,对于这道题x1=3, x2=5, x3=9, x4=17, x5=33, 因此
X2-X1=2–>2^1
X3-X2=4–>2^2
X4-X3=8–>2^3
X5-X4=16–>2^4
...
X20-X19=2^19
这样解题又快速又便捷!
第100项题/前100项和(大项题)
看完第二类题,让我们来看看最有意思的第三类题,这类题目往往涉及到求第100项,1000项,甚至2000项或者前100项,1000项,甚至2000项的和。像这种项数比较大的题,同学在拿到时就应明确的思路是这个题一定是有规律的,规律:
- 要么是等差等比数列,直接套用公式

- 要么是循环数列,去找循环结
那么对于这道题,我们看到求前100项和,又无法得出等差或者等比的结论,直接找规律(需要注意的是,有些题目循环结比较长,甚至能达到8~10个,同学们一定要有耐心,如果算了很多还没算出循环,估计你是算错了)
对于这道题
A1=-5, A2=4, A3=9, A4=5, A5=-4, A6=-9, A7=-5
所以我们可以得出这个数列6个一循环,且每个循环的和为0,那么前100项一共包括16个循环,第17个循环到第4位,也就是前四项的和。因此前100项和为13。
所以日后,同学们在拿到数列题时候可以尝试通过以下思维导图来引导自己的解题思路
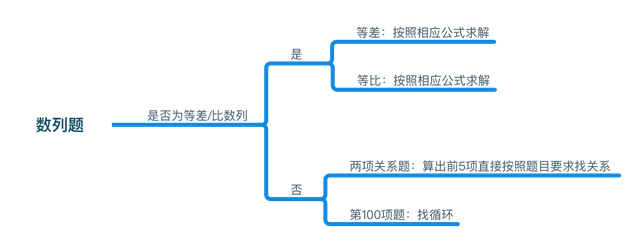
像数列题一样,GRE考试中大部分数学题是有规律的,同学们可以多做题多总结。
姜仁君,北京新东方GRE数学老师,毕业于伦敦政治经济学院国际管理专业,跨多科目教学,拥有丰富的GMAT,GRE数学课堂经验,帮助多位学员拿到GMAT数学51,GRE数学170的分数。
各位备战托福的同学,欢迎加入新东方托福备考QQ群(113130831),我们将在群内定期分享考试最新动态及新东方独家备考资料,期待你的加入哦!

最新热文推荐:
(责任编辑:Hui)



